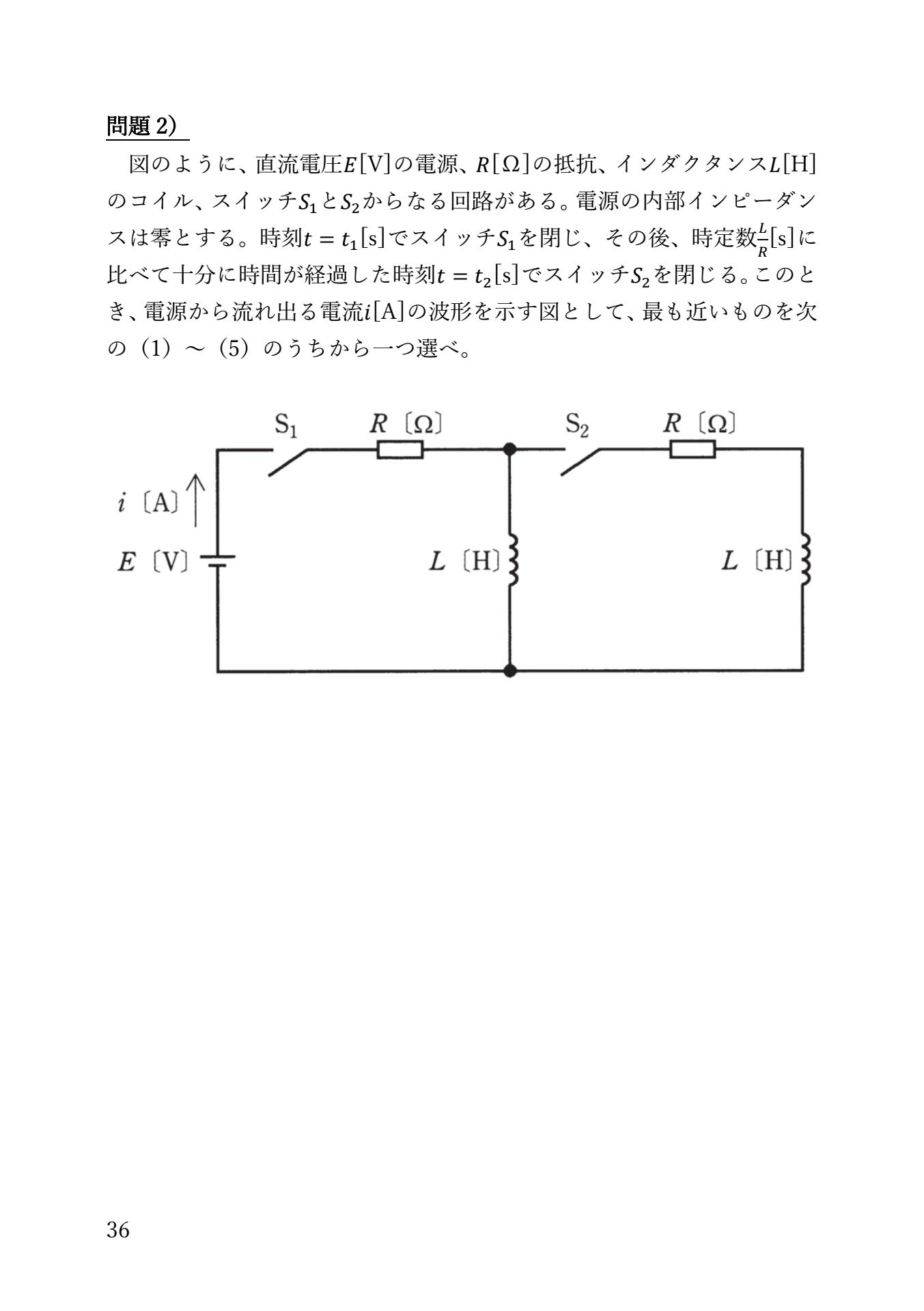
電験3種 理論 過渡現象の公式を紹介します!
過渡現象は、覚える公式が少ないので、得点源につながりやすい分野です。
どの過去問も、以下の公式だけで解くことができるので、マスターすれば心強いです。
その反面、正確な現象理解が必要になるほか、どの公式を、どの場面で使うのかを完璧に仕上げなければなりません。
キッチリと、公式の意味までマスターしておきましょう。

この記事では、
電験参考書を作成しいている立場から、電験3種の出題傾向を分析していますよ!
過渡現象は難しいのか
過渡現象とは、電圧源や電流源、加えて抵抗やコイル、コンデンサが接続された回路において、電圧や電流の時間変化を考える分野です。
過渡現象で重要なのは、なんといっても数学力。
過渡現象の応答式は、
$$i=\frac{E}{R}\left(1-e^{-\frac{R}{L}t}\right)$$
や、
$$v=Ee^{-\frac{1}{RC}t}$$
というような、難しい数式が出てくる他、微分・積分といった高度な数学知識が必要になります。
なので、過渡現象を理解するには、まずは、数学力を磨かないといけません。

数学は苦手・・・
じゃあ、私には電験3種、無理なのかな・・・

そんなことはないですよ。
電験3種の合格には、イメージ重視の理解で十分です。
このまま読み進めてみてね。
【たったこれだけ!】電験3種 過渡現象の公式
本気で理解するには、数学力が必要な過渡現象。
しかし、電験3種であれば、公式を使いこなせれば十分解けます。
冒頭でも書きましたが、過渡現象は、使う公式が限られているので得点源になりやすい分野です。
ぜひ公式をマスターし、過渡現象を得点源に変えましょう。
初期状態と定常状態
コイル・コンデンサの初期状態と定常状態は、以下の通りになります。
| 初期状態 | 定常状態 | |
| コイル | 開放 | 短絡 |
| コンデンサ | 短絡 | 開放 |
時定数の計算
$RL$回路、及び$RC$回路の時定数$\tau$は、
$$\tau=\frac{L}{R}=CR$$
となります。
応答波形のイメージ
これに加えて、応答波形のイメージを理解できていれば十分でしょう。
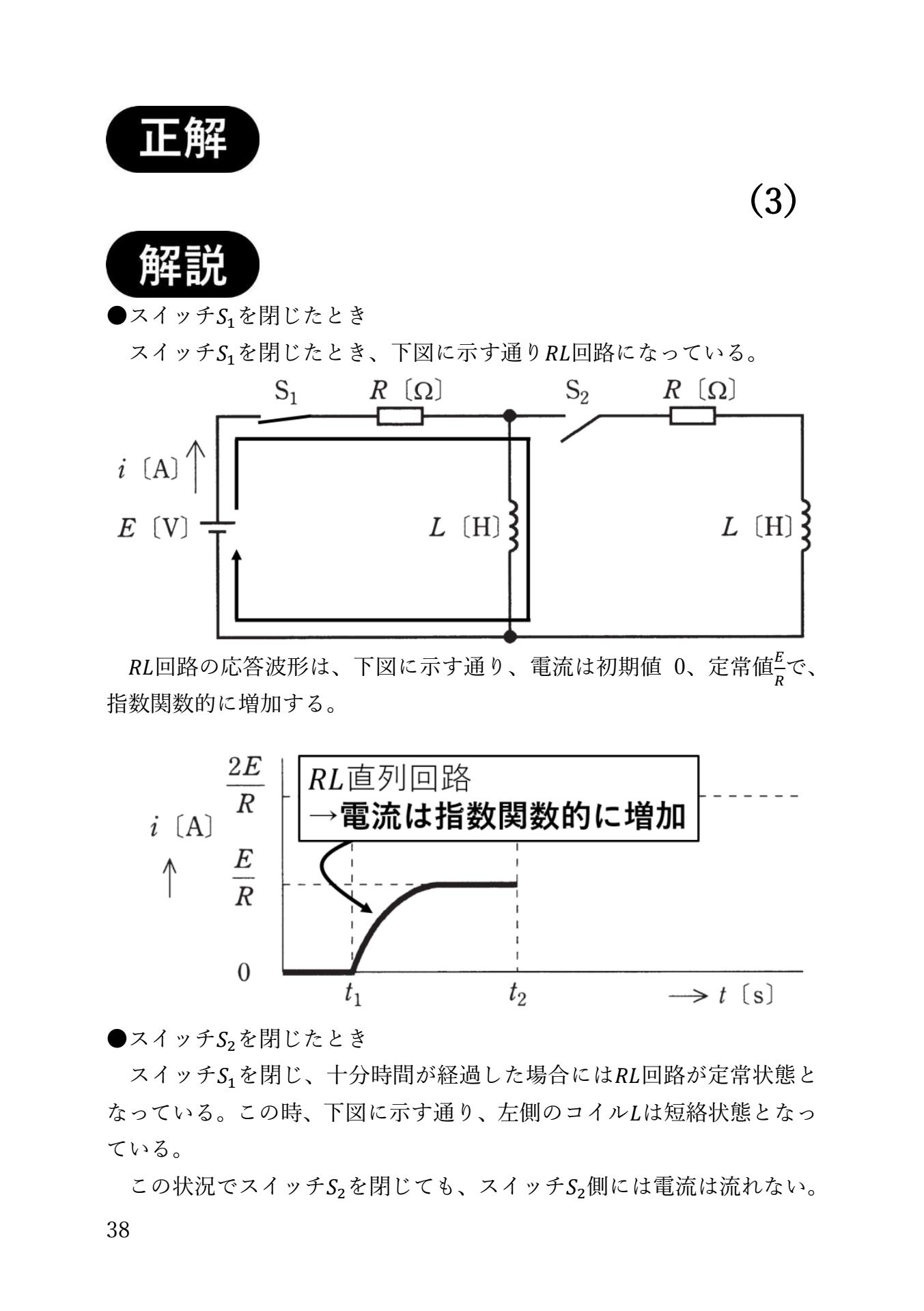
RL回路
$RL$回路の電流は指数関数的に増加する。
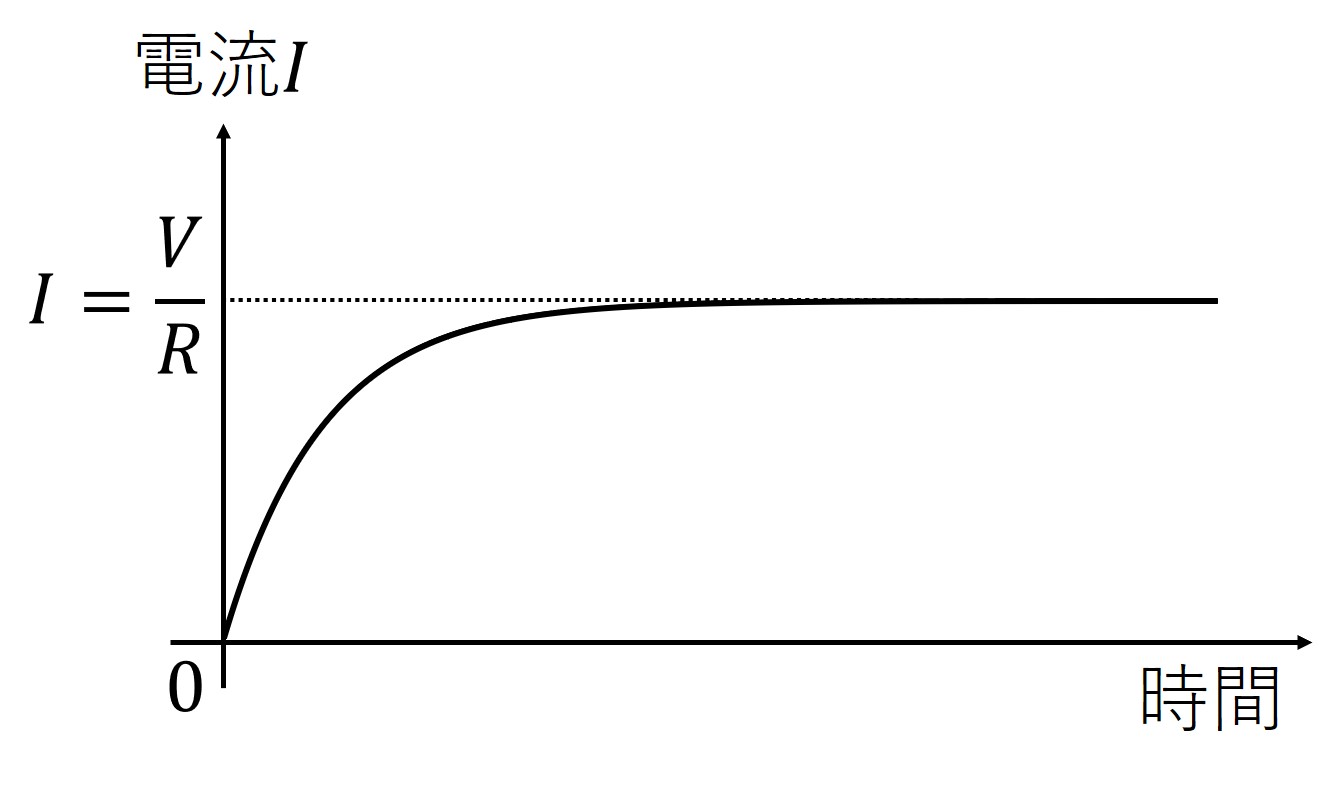
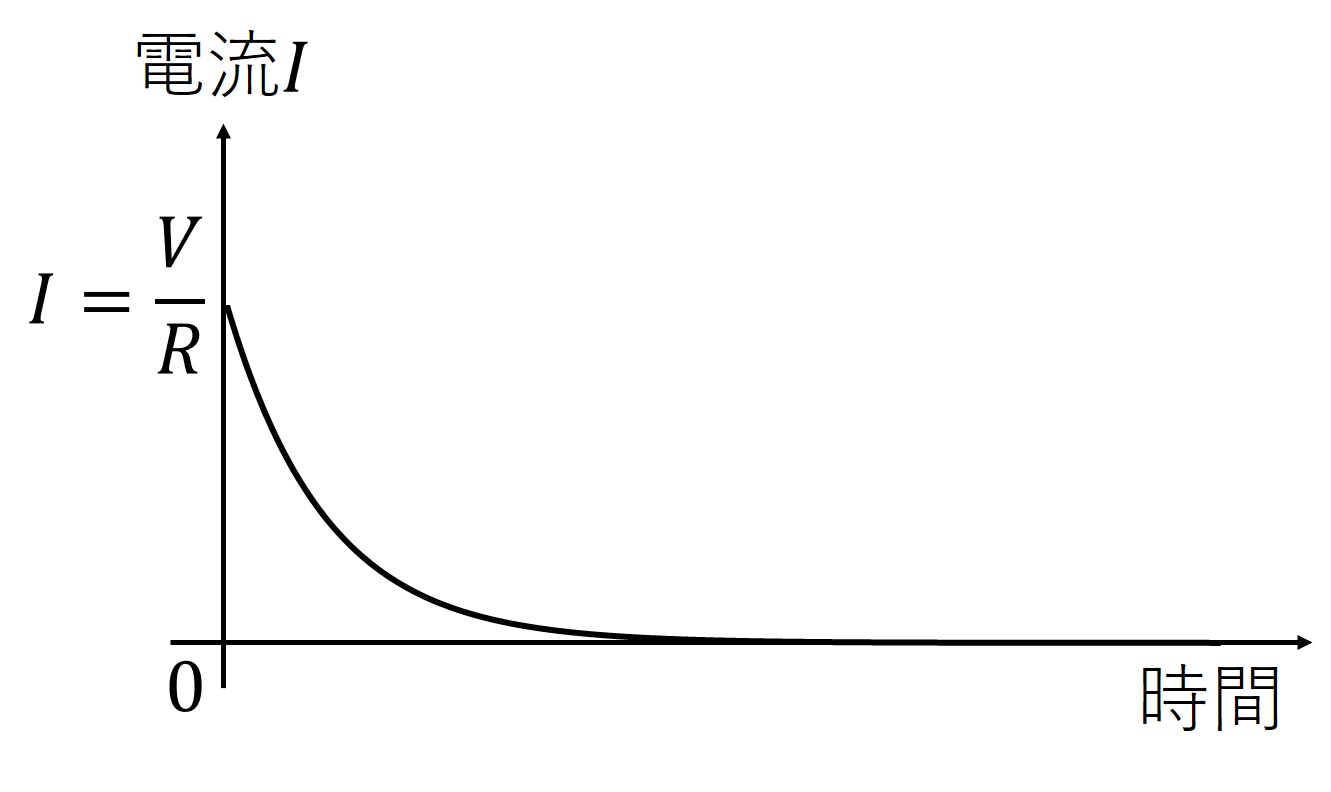
RC回路
$RC$回路の電流波形は指数関数的に減少する。

この通り、電験3種の過渡現象だけなら、意外と簡単に解けますよ。
必要なのは分数の計算力ぐらい。
微分・積分が必要なのは、電験2種からです。
ただし、「公式の暗記」では合格は難しい
過渡現象の公式は非常に少ないですが、暗記しただけでは得点につながりません。
過去問で、どの公式がどのように使われているのかを理解しないといけません。
例えば、過渡現象における応答波形の意味なども、正確に理解しなければなりません。
公式の暗記だけでは、少し難しい問題になってしまうと、すぐに解けなくなります。

例えば、
●過渡現象って、そもそも何?
●上に書いた応答波形の意味
を、自分の言葉で説明できるか、考えてみよう!
【1週間の集中対策】過渡現象を得点源にする方法
さて、過渡現象はしっかり基礎を身につけ、自力で過去問を解けるよう、念入りに対策しなければなりません。
しかし、仕事の合間に勉強するとなると、勉強する時間も限られています。
そこで、この参考書を使って、1週間だけ頑張ってみましょう。
著者:電験合格プロジェクト
内容:1週間の集中対策で過渡現象を得点源に
図解が多く、イメージ重視
難しい数式・専門用語は使わない!
文系・初学者に最適
図解イメージで理解できる!
過渡現象を、水の流れを用いて直感的理解を促します。
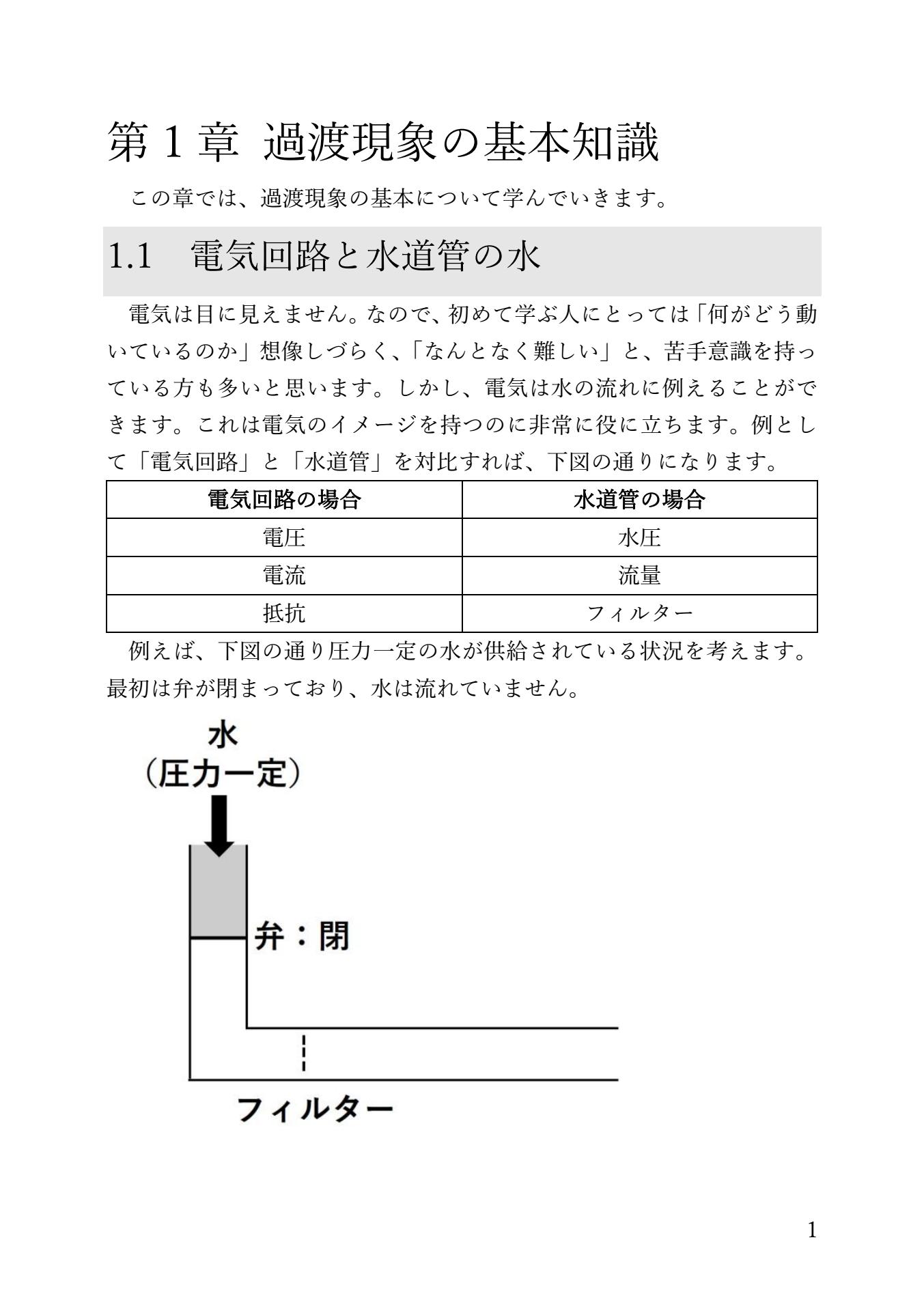 |
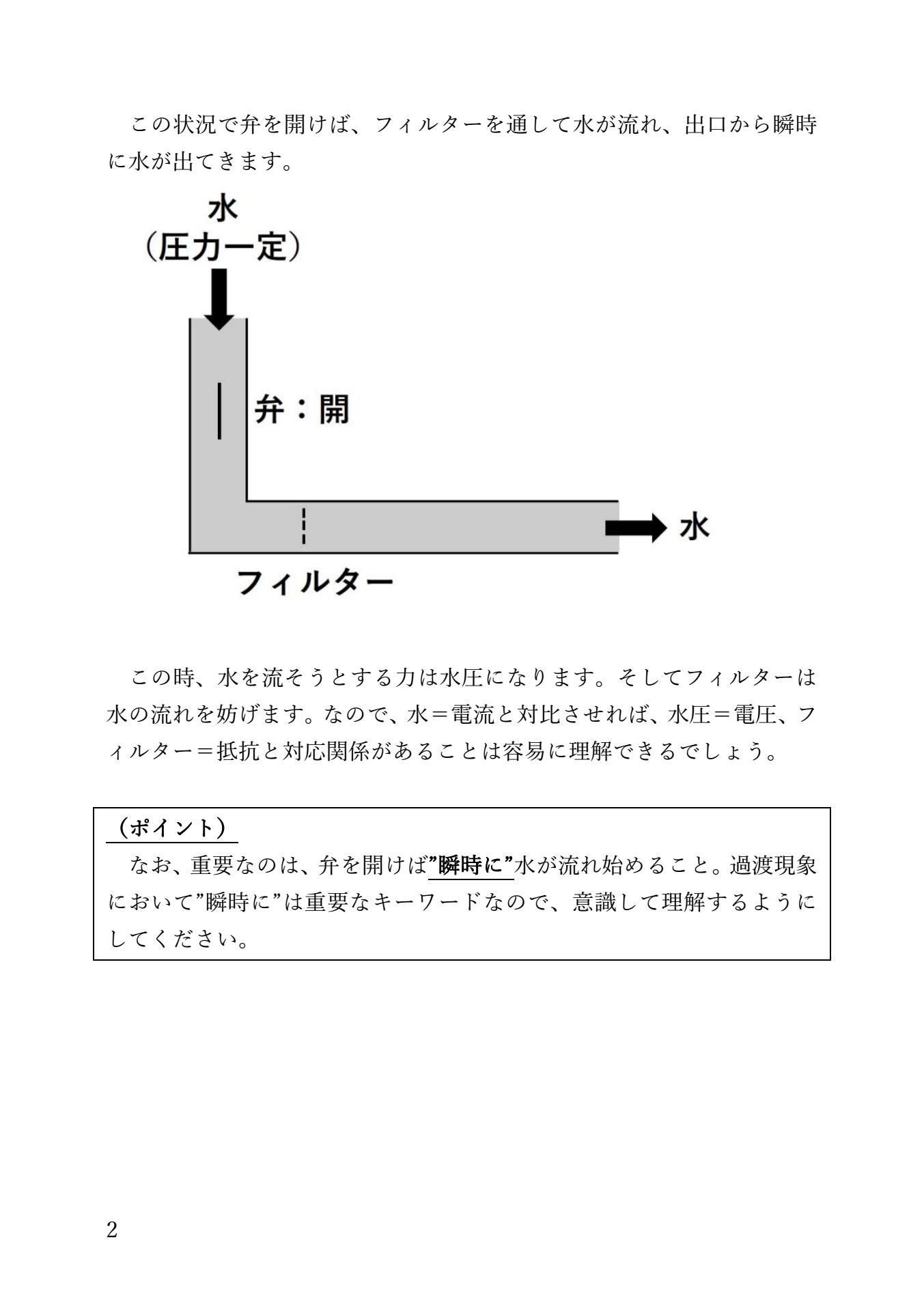 |

まずは数式よりも、図解が大事。これは絶対です。
豊富、丁寧な過去問解説!
過去問もたくさん収録。
加えて、丁寧な解説で、公式の使い方まで、完全にマスターできます。
 |
 |

電験3種の基本は過去問対策。
キッチリ解説しているので、過渡現象を制覇できます。
難しい数式・専門用語は一切ナシ
多くの参考書にある、
- 言葉の意味は何?
- この式は何?
といった、躓く部分を徹底的に取り除きました。
挫折を招く原因を排除しているので、誰にでも過渡現象が理解できます。

「初学者向け」って言いながら、
●知らない言葉が突然出てきたり
●難しい数式が出て着たり
今の参考書は、もう挫折しそう・・・

大丈夫!
本気で初学者に向き合うために、「専門用語なんて使わない」を徹底しています。
まとめ
ここまで、過渡現象の重要公式について紹介してきました。
過渡現象は、覚える公式が少ないので、得点源につながりやすい分野です。
その反面、正確な現象理解が必要になります。
もし、過渡現象に自信がない方は、この参考書を使って対策してください。
繰り返しますが、まずは1週間だけ頑張ってみてください。
きっと、過渡現象が得意になるはずです。
著者:電験合格プロジェクト
内容:1週間の集中対策で過渡現象を得点源に
図解が多く、イメージ重視
難しい数式・専門用語は使わない!
文系・初学者に最適



